"On mechanical slavery, on the slavery of the machine,
the future of the world depends."Oscar Wilde, The Soul of Man Under Socialism, 1895
In this introduction we will look at some building blocks of organisation, both in terms of life (real and artificial) and in the structure of inorganic materials. We will investigate Cellular Automata and relate these to computers, brains and cells, plus speculate on the future goals of nanotechnology.
Firstly what exactly is an automaton ? Most people will recognise the word as one applied to a mechanical toy that emulates some apparently living behaviour. Within our field this is generalised to any system that has a finite number of internal states and moves between those states by following specified rules - this is a form of mapping (input to output, similar to a computer program). An automaton is also an agent in ALife terms, although agents can also occur in many other forms. An agent is an entity that can interact with its surroundings and usually changes its own state as a result. If we bring together a collection of such agents and allow them to interact then we have an automata system.
If we assume automata to be fixed (not mobile) we can equate them with cells in a structure. This structure could be living,
molecular, mechanical - any form in fact. This gives us a Cellular Automata (CA), a structure that, whilst static in physical
form and space, can exhibit dynamic behaviour in time - emergent order.
Let's take a simple case, a board divided into small squares (a lattice). Each square can be in either of two states (black or white). We colour each of the squares initially either black or white at random. For each square, if it starts black then it stays black if two or three of its 8 neighbours (including diagonals) are also black, otherwise it changes to white. If it starts as white then it stays white unless exactly three of the neighbours are black, then it changes to black. We evaluate the current state of all the squares and determine what they will do next, then we change the whole board accordingly. This is called a step (or cycle, or generation). We then repeat the exercise over and over (iterate). The pattern in time that we see of changing square colours proves hard to predict, although every square follows the same simple rules. We can extend such systems to have many individual states per cell, to have transition rules of any complexity and to depend on non-neighbouring events for these rules. All are Cellular Automata.
The example I gave, despite its simplicity, is one of the most powerful known and is usually called the "Game of Life"
after its inventor John Conway. The rules are clearer if we regard the black cells as alive. Thus having 3 alive neighbours
allows a new birth (parents + midwife!), having over 3 gives death from overcrowding, and under 2 death from exposure.
The patterns that can arise from certain starting positions are complex and fascinating, and many computer programs
are available to generate and investigate them (e.g. LIFE32).
One of the most interesting findings is that such a system can perform arithmetic, including logic, and thus it is possible
to build a computer from a sufficiently rich pattern of cells. In fact some CAs (including Conway's Life) are what is known
as Universal Computers, they are capable of any task, including reproduction, given an appropriate initial pattern (program).
One feature of interest is that these systems are discrete, not continuous functions. Unlike most systems studied in science and mathematics our functions here are stepped, they change in fixed intervals of time. It makes no sense to consider an in-between generation - the change from one state to the next is assumed to occur instantaneously. This means that conventional techniques for determining rates of change (differentiation) or dynamics are not directly applicable.
The Game of Life is a CA in two dimensions, however we can generalise to fewer or more dimensions. Most detailed analysis has been done on one dimensional CAs (1D), where we only need consider neighbours to left and right. For these the second dimension used is that of time, so we are able to visualise the development of the system and display it as a picture. Two dimensional systems (2D) have much greater complexity and can only be visualised by watching them evolving in time or by abstracting desired features for display. Going beyond this to a 3D system creates many problems, although in real life these are the most common types (multi-cellular organisms) - we still have much to learn here.
To appreciate the complexity of this task we need also to consider the rules. There are vast numbers of possible rules for systems above one dimension, but even in 1D we can specify many different ways of determining the next state. The usual method is to total the states of the relevant neighbours and determine the new state from the sum (Totalistic CAs). The Game of Life operates in this way, needing 3 neighbours in total to give life. The scope of our neighbourhood can be local (touching), close (including neighbour's neighbours) or global (anywhere in the system). We can restrict the interactions to few neighbours (sparse connectivity), to them all (full connectivity) or somewhere in between. We can use random neighbours or those chosen by some logic. We can specify the transition or state tables (the rules) to any degree of complexity. Some rule schemes will conserve certain properties of the system (e.g. the number of live cells) - these systems are reversible and mimic typical physical systems (like atoms in a box). Other schemes allow the cells to grow or die out - these better mimic living systems. Complications of these sorts take us also into the areas of Boolean Networks and Neural Nets.
The various types of CA fall into 4 Classes (defined by Stephen Wolfram).
Class 4 - structured. System can develop in highly patterned but unstable ways. Computationally rich, e.g. the Game of Life. This denotes an automata between states 2 and 3 - at the edge of chaos, as we call it.
The type of behaviour found for a particular CA depends upon the structure of the rules employed. For Class 4 behaviour a cell state should change between 25% and 50% of the time (Langton's lambda parameter), depending on ruleset, less than this generally leads to static behaviour (Classes 1 & 2), more to unstructured behaviour (Class 3). These classes have equivalents in higher dimensional inorganic and living systems, especially Type 4.
So far we have been interested in uniform systems when the same rule applies to all the cells (global or homogeneous rules). If we instead allow for each cell to have a different set of rules (non-uniform or heterogeneous cells), we then have a collection of cells which may differ in behaviour and are close to the realms of Cellular Programming - parallel co-evolution. This and other techniques come under the auspices of Evolutionary Computation (see FAQ).
Suppose now that we also relax the movement restriction, we then have the more general form of automata used in Artificial Life, and often referred to as Agents or even Creatures. Each agent can react in a specified way to the environment (which includes the other agents). These actions can now take more familiar forms, movement (towards food, away from danger), eating (building energy reserves), reproduction (division), communication (passing messages) and so on.
If the agents have a fixed number of states then they are Finite State Machines, but this restriction also can be relaxed. We can allow the agents to learn, storing any useful data they accumulate. Their next state can then depend also upon historical data - we have the possibility of anticipation and planning. Ultimately we can envisage a creature that can create new states, new behaviours. From simple beginnings, via simple steps, we can go from immobile, causal, simplistic entities to complex, mobile, thinking ones - mimicking evolution perhaps.
Can we claim therefore that humans are perhaps a form of automata ? Strange though it may appear some evidence supports this. Every cell in our body contains a structure known as a cytoskeleton, this as the name implies forms the backbone to the cell shape. The structure of this skeleton comprises microtubules which seem to organise the cell activities - a cellular nervous system maybe. The molecular protein sub-units of these tubules seem to demonstrate automata behaviour, suggesting that the basis of life may indeed be such forms of organisation.
Perhaps we can also extend this to matter ? Some work on the interactions of inorganic objects, atoms, rocks, galaxies treats these as forms of automata or computational systems. Applications as diverse as fluid flows, image processing and urban development have been modelled in the form of CAs, together with more traditional cellular shaped subjects.
It is known that our cells communicate with each other by chemical and other means, so that perhaps our multicellular structures are just higher level automata ? Taking this to the limit we can apply the same ideas to thought (brain neural automata) and society (people as agents). Of course such thinking does not reduce the majesty of our human intelligence one iota, all automata are just building blocks (as are atoms) - the emergent patterns that appear from the interactions are themselves the mystical events. CA thinking does give however a better (perhaps correct) way of explaining the method in which structure arises - a richer methodology than that available from the traditional reductionist sciences.
Take for example the flocking of birds. Does each bird perform a complex communication and analysis calculation
to determine how to fly in formation ? No, such calculations are not possible in the time available, even for creatures
like ourselves. Simulations based upon CA techniques have shown that a few simple rules automatically applied
can explain such emergent behaviours. The simplest one is just stay a fixed distance from your neighbour - the lead
'bird' then will command the flock, all the rest will adjust their position to maintain a relative pattern. Such instinctive
(unconscious) action is easy to envisage arising by natural selection. Either bunching or isolation would make survival
from predators more unlikely.
We have largely been considering automata as the basis for life, but recall that we started with an inorganic pattern of squares to which we applied the rules externally. Could such secondary CAs occur in nature ? At an inorganic level we simply need a system comprising multi-state entities and some method of changing those states contextually. Molecules, particularly big ones, have many natural orientations or shapes. Could we impose rules on these from outside, as we did with the squares ? Suppose we fabricated a system comprising an assembly of molecules in the form of a simple computer, could we then arrange the system such that it reacted to its environment and acted upon it in a known way ?
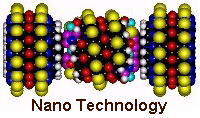What we have described is the basis of nanotechnology, the idea that we can duplicate large scale machines at
molecular level. You will recall that a CA can be a universal computer so can emulate any machine we may wish
to construct. By using molecular engineering it now seems possible technically to create inorganic entities that
function in a very similar way to that occurring within our own cells, and are comparable in size to our own proteins.
What function could such systems perform ? Well, our body has limited ability at self repair. If we are able to manufacture new body components, on site within our own cells, then we have the potential to reverse ageing - effective immortality. Outside the body a Universal Replicator (a constructional equivalent of the Universal Computer) could create food directly from the base molecules, using sunlight as power - an artificial plant. The same process could feasibly create all our material needs in the same way, totally free - an end to poverty ?