These pages show examples of the sorts of pictures generated within the complexity sciences. Many of these pictures are artforms in their own right and this association has led to a merging of the disciplines of the arts, sciences and mathematics within the complex systems field. The visualisation of research simulations by computer graphics is one of the main methods we have of investigating emergent phenomena. To navigate through the pages in turn press the button, or to select a particular page directly use the links at the bottom of the page. Press to return to this page or for the previous page. If you are more artistically inclined you may wish also (or instead) to visit our
Complex Art Exhibition of traditional paintings.
This first set of images are Fractals generated using the FRACTINT program which is available free from many sources. Many forms of fractal are possible, the current V20 DOS program lists 106 basic types, each with almost infinite choice of settings. The space of possible fractals is so vast that only a few have ever been found.
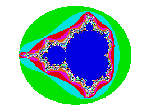
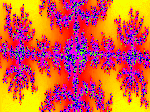
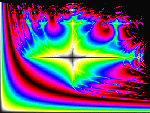
In order, they are a) A standard Mandelbrot set, b) A Julia Spiral closeup, c) Candles - Julia cross,
d) Satrings - Rossler3D attractor looking like Saturn's rings, e) Trilobite - Quatjul discovery of a fossil,
f) Lyapun2 - Lyapunov 2D bifurcation type, g) Newton7 - fractal roots of x to power 6,
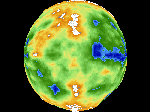
h) Planet - Spherical transform of a plasma type fractal
Symmetrical Icons are a fractal type that has many correspondences with traditional art, particularly religious and meditational forms. Structure arises by plotting chaotic dots and the image appears as if by magic.
IconTri2, IconSqr, IconPent and IconWhel. Icon type fractals of symmetries a) 3, b) 4, c) 5, and d) 29 sides
The 4 below are also icons and represent the various forms of attractor that result from small changes to one of the parameters. This sensitivity to initial conditions is crucial in Chaotic attractors of this type.
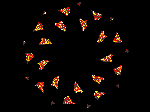
Mind6, Mind8, Minda and Mindzom6.
Lambda values of a) 1.794, b) 1.814, c) 1.894 and d) a zoom of the structure of one disjoint element
Cellular automata (finite state machines) are lattices of independently behaving cells, here in 1 or 2 dimensions. Each cell only pays attention to its immediate surroundings, the overall pattern that we see is emergent and not programmed.
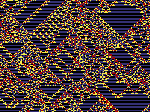
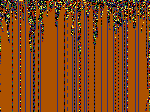
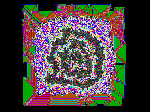
a) CAr51r1 - Structured 1D CA, forever changing, b) CAr61r9 - 1D CA that settles to repeat cyclically,
c) Ant City - 2D Growing population, d) Mite7 - 2D Geometric lifestyle of a artificial mite.
Most of the above images can be generated for yourself in high resolution, using the parameter file option from FRACTINT. Some of these are generated by using par files made generally available by other people. The necessary parameters can be downloaded from here PARMFILE. This contains the author credits for all these pictures along with their original source locations (if any).
The following images are from the Fractal Vision system (book and program by Dick Oliver, pub SAMS) which iterates a fractal template (IFS) to build a recognisable image from small very simple copies of itself. This is the opposite of fractal compression and gives emergent patterns from a seed, usually consisting of just a few straight lines..
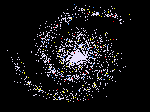
a) Flowering cherry tree, b) A spiral galaxy, c) Hen sat on a nest, d) Koch snowflake
Complex mappings - order from chaos, use simple formulae iterated over and over to produce the visible structure. Boolean nets self-organise themselves dynamically by having logic gates connected to each other at random, the system settles down over time into a stable structure.
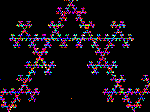
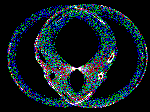
a) Simple 3 point shift pattern,, b) Chirikov Map chaotic pattern,
c) Logistic map showing bifurcation, d) Boolean NAND network self organisation
Artificial Life systems show evolution in action with genetic mutation, sexual crossover and fitness selection . They use collections of agents (entities) that interact and develop emergent behaviours, similar to those we find in real life.
a) Ant trails for competing species, b) Cyclic food chain of 15 species, c) Coevolution of herbivores and plants,
d) Flocking of birds, e) Semi-totalistic automata evolution, f) Mice evolving to locate food,
g) A Biomorph moth, h) Space covering with symmetrical icons
Software is freely available for most of these tasks. See the various FAQs for details.