Most equations with which we are familiar have simple solutions, they either converge to a fixed value or to a limited number of such values. Here we enter a different world, a world dominated by chaos, yet strangely predictable. The images on this page are second order equations (squares and lower terms) of the three variables x, y and z (3 dimensional), where each variable depends on the other two. This interconnection leads to chaotic solutions, where the variables follow each other in an endless dance over the solution space. In these images the x and y dimensions are horizontal and vertical, the z dimension is colour coded into 256 representative levels (ranges of values).
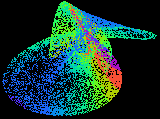
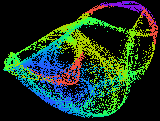
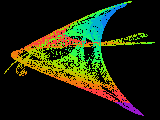


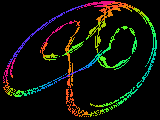
It is seen that the solutions are all contained within a definite figure, which we call the 'strange attractor'. In these objects no solution ever repeats exactly, yet a solution will approach another over and over again, throughout infinite time. The equations are perfectly deterministic, yet sensitivity to initial conditions means that we cannot predict any solution more than a short time into the future. The trajectory jumps all over the attractor space, carving out a semi-solid pattern at times, a tracery at others, forming disconnected islands at yet other parameters. A minor change to one parameter can switch the solution to a very different looking attractor, collapse it to a fixed solution or vice-versa. An apparently well behaved equation can suddenly erupt into an infinitely complicated chaotic structure, yet one containing much embedded order.

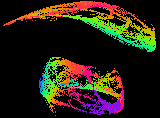
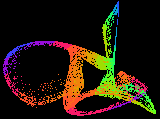



One feature of attractors such as these is that initial values outside the structure are sucked into the attractor, and then can no longer escape (rather like a black hole). The region for which this is true is called the basin of attraction, and the trajectory of a point until it reaches the attractor is called the transient.


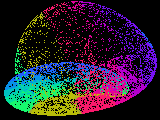



These structures are dynamical, the value of the variables never stops changing, yet they are also static, the form of the attractor never changes. This latter feature means that they are predictable in statistical terms, we can determine for any small region of the attractor what the probability is that the system will be found there, very similar to the methods used in Quantum Theory. At the same time, knowing an instantaneous value we can predict almost exactly the next few values, also similar to the methods of Newtonian science.
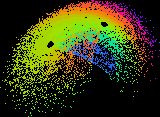


The software to produce these attractors and many others can be obtained from Sprott's Software